At HSR, I'm currently enrolled in a course about neural networks and machine learning. One of the simplest forms of a neural network model is the perceptron.
Background Information
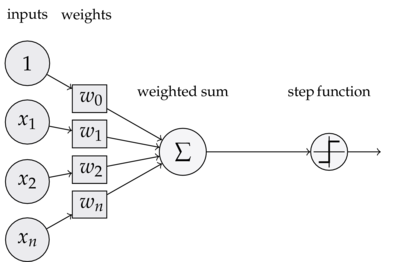
A perceptron classifier is a simple model of a neuron. It has different inputs ($x_1$...$x_n$) with different weights ($w_1$...$w_n$).
The weighted sum $s$ of these inputs is then passed through a step function $f$ (usually a Heaviside step function).
To make things cleaner, here's a little diagram:
Python!
Here's a simple version of such a perceptron using Python and NumPy. It will take two inputs and learn to act like the logical OR function. First, let's import some libraries we need:
from random import choice
from numpy import array, dot, random
Then let's create the step function. In reference to Mathematica, I'll call this function unit_step.
unit_step = lambda x: 0 if x < 0 else 1
Next we need to map the possible input to the expected output. The first two entries of the NumPy array in each tuple are the two input values. The second element of the tuple is the expected result. And the third entry of the array is a "dummy" input (also called the bias) which is needed to move the threshold (also known as the decision boundary) up or down as needed by the step function. Its value is always 1, so that its influence on the result can be controlled by its weight.
training_data = [
(array([0,0,1]), 0),
(array([0,1,1]), 1),
(array([1,0,1]), 1),
(array([1,1,1]), 1),
]
As you can see, this training sequence maps exactly to the definition of the OR function:
| A | B | A OR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Next we'll choose three random numbers between 0 and 1 as the initial weights:
w = random.rand(3)
Now on to some variable initializations. The errors list is only used to store the error values so that they can be plotted later on. If you don't want to do any plotting, you can just leave it away. The eta variable controls the learning rate. And n specifies the number of learning iterations.
errors = []
eta = 0.2
n = 100
In order to find the ideal values for the weights w, we try to reduce the error magnitude to zero. In this simple case n = 100 iterations are enough; for a bigger and possibly "noisier" set of input data much larger numbers should be used.
First we get a random input set from the training data. Then we calculate the dot product (sometimes also called scalar product or inner product) of the input and weight vectors. This is our (scalar) result, which we can compare to the expected value. If the expected value is bigger, we need to increase the weights, if it's smaller, we need to decrease them. This correction factor is calculated in the last line, where the error is multiplied with the learning rate (eta) and the input vector (x). It is then added to the weights vector, in order to improve the results in the next iteration.
for i in xrange(n):
x, expected = choice(training_data)
result = dot(w, x)
error = expected - unit_step(result)
errors.append(error)
w += eta * error * x
And that's already everything we need in order to train the perceptron! It has now "learned" to act like a logical OR function:
for x, _ in training_data:
result = dot(x, w)
print("{}: {} -> {}".format(x[:2], result, unit_step(result)))
[0 0]: -0.0714566687173 -> 0
[0 1]: 0.829739696273 -> 1
[1 0]: 0.345454042997 -> 1
[1 1]: 1.24665040799 -> 1
If you're interested, you can also plot the errors, which is a great way to visualize the learning process:
from pylab import plot, ylim
ylim([-1,1])
plot(errors)
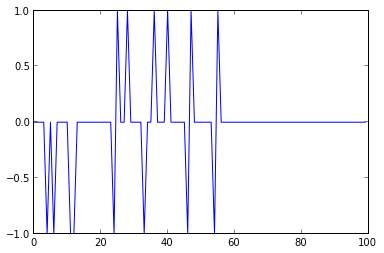
It's easy to see that the errors stabilize around the 60th iteration. If you doubt that the errors are definitely eliminated, you can re-run the training with an iteration count of 500 or more and plot the errors:
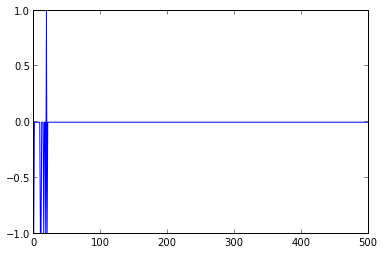
You could also try to change the training sequence in order to model an AND, NOR or NOT function. Note that it's not possible to model an XOR function using a single perceptron like this, because the two classes (0 and 1) of an XOR function are not linearly separable. In that case you would have to use multiple layers of perceptrons (which is basically a small neural network).
Wrap Up
Here's the entire code:
from random import choice
from numpy import array, dot, random
unit_step = lambda x: 0 if x < 0 else 1
training_data = [
(array([0,0,1]), 0),
(array([0,1,1]), 1),
(array([1,0,1]), 1),
(array([1,1,1]), 1),
]
w = random.rand(3)
errors = []
eta = 0.2
n = 100
for i in xrange(n):
x, expected = choice(training_data)
result = dot(w, x)
error = expected - unit_step(result)
errors.append(error)
w += eta * error * x
for x, _ in training_data:
result = dot(x, w)
print("{}: {} -> {}".format(x[:2], result, unit_step(result)))
If you have any questions, or if you've discovered an error (which is easily possible as I've just learned about this stuff), feel free to leave a comment below.